14 Evaluación de impacto: ¿realmente funcionó?
14.1 La pregunta más importante (y más difícil) de las políticas públicas
Imagina que un gobierno implementa un programa de transferencias condicionadas para reducir la pobreza. Cinco años después, la pobreza bajó. ¿Funcionó el programa?
La respuesta honesta: no tenemos idea. La pobreza pudo haber bajado por el crecimiento económico, por otros programas, por migración, por mil razones. Que dos cosas ocurran al mismo tiempo (el programa y la reducción de pobreza) no significa que una cause la otra. Ya lo dijimos: correlación no es causalidad.
La evaluación de impacto es el conjunto de métodos diseñados para responder la pregunta causal: ¿cuál es el efecto del programa específico sobre el resultado que nos interesa? Es la joya de la corona de la investigación cuantitativa aplicada, y entenderla cambia completamente la forma en que lees los titulares sobre “programas exitosos” (Gertler et al., 2016).
Y no es solo para economistas. Si investigas en educación, salud, desarrollo, política social, medio ambiente, o cualquier área donde se implementan intervenciones, necesitas entender evaluación de impacto. Aunque no la hagas tú mismo, necesitas poder leer críticamente las evaluaciones que otros hacen.
14.2 El problema fundamental: el contrafactual
El corazón de la evaluación de impacto es un concepto simple pero profundo: el contrafactual. ¿Qué habría pasado si el programa no hubiera existido?
El problema es que no podemos observar el contrafactual directamente. No podemos ver a la misma persona en dos universos paralelos: uno donde recibió el programa y otro donde no. Por eso necesitamos métodos creativos para construir un contrafactual creíble.
Formalmente, el efecto causal del programa para un individuo \(i\) es:
\[\tau_i = Y_i(1) - Y_i(0)\]
Donde \(Y_i(1)\) es el resultado con el programa e \(Y_i(0)\) es el resultado sin el programa. Solo podemos observar uno de los dos. Al otro se le llama el resultado potencial no observado. Esta es la base del marco de resultados potenciales de Rubin, que Angrist & Pischke (2009) formalizan magistralmente.
Como no podemos calcular \(\tau_i\) para cada individuo, buscamos el efecto promedio del tratamiento (ATE):
\[ATE = E[Y(1) - Y(0)]\]
O, más frecuentemente, el efecto promedio sobre los tratados (ATT):
\[ATT = E[Y(1) - Y(0) | D = 1]\]
Todo lo que sigue son diferentes formas de estimar estas cantidades de manera creíble.
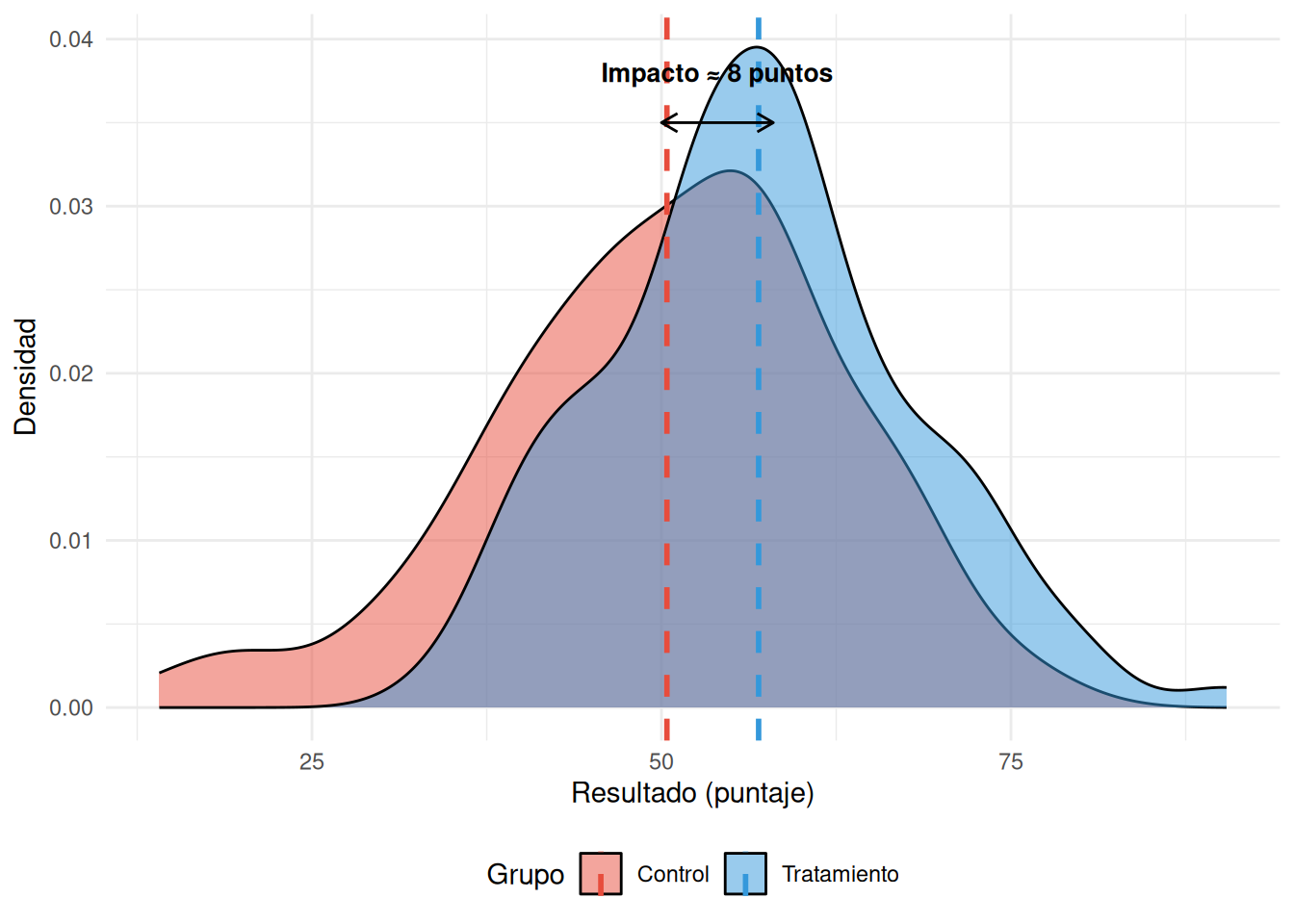
14.3 Experimentos aleatorios (RCTs): el estándar de oro
14.3.1 ¿Cómo funciona?
Asignas aleatoriamente a los participantes en dos grupos:
- Grupo de tratamiento: Recibe la intervención.
- Grupo de control: No la recibe (o recibe el statu quo).
Como la asignación es aleatoria, los dos grupos son estadísticamente iguales en promedio en todas las características observables y no observables. Cualquier diferencia en los resultados se atribuye al programa.
14.3.2 Ejemplo clásico
El programa PROGRESA (México, hoy Oportunidades/Prospera) fue evaluado con un RCT. De 506 comunidades elegibles, 320 fueron asignadas aleatoriamente a recibir el programa y 186 como control. Los resultados mostraron efectos positivos en matrícula escolar, salud y nutrición. Porque fue un RCT, esos efectos son causalmente creíbles.
Otro ejemplo fundamental: J-PAL (Abdul Latif Jameel Poverty Action Lab) ha coordinado cientos de RCTs en países en desarrollo, generando evidencia sobre qué funciona en educación, microfinanzas, salud preventiva y más. Su trabajo demostró que las redes tratadas con insecticida son más efectivas para prevenir malaria que muchas intervenciones más caras.
14.3.3 ITT vs. TOT: lo que asignas vs. lo que recibes
Aquí hay una distinción crucial que muchos ignoran:
- Intention to Treat (ITT): Comparas según la asignación al tratamiento, independientemente de si la persona realmente lo recibió. Si asignaste a alguien al grupo de tratamiento pero nunca fue al programa, sigue contando como tratado.
- Treatment on the Treated (TOT): Comparas solo a quienes efectivamente recibieron el tratamiento con el grupo de control.
¿Cuál usar? ITT es más conservador y preserva la aleatorización. TOT puede estar sesgado (los que cumplen pueden ser diferentes de los que no). En la práctica, se reportan ambos. El ITT te dice cuál es el efecto de ofrecer el programa; el TOT te dice cuál es el efecto de recibirlo.
NotaPara recordar
En América Latina, el cumplimiento imperfecto (non-compliance) es la norma, no la excepción. Beneficiarios que no cobran transferencias, familias que no llevan a sus hijos a los controles de salud, escuelas que no implementan el currículo nuevo. El ITT captura esta realidad; el TOT la ignora.
14.3.4 El concepto LATE
Angrist & Pischke (2009) introdujeron un concepto fundamental: el Local Average Treatment Effect (LATE). Cuando hay incumplimiento, lo que estimas con variables instrumentales no es el efecto promedio para toda la población, sino el efecto para los compliers (los que cumplen según les asignan).
Esto importa porque los compliers pueden ser muy diferentes de la población general. El efecto de un programa de tutoría para los que asisten regularmente puede ser muy distinto del efecto para quienes nunca irían.
14.3.5 Limitaciones (que los fanáticos de los RCTs no te cuentan)
- Ética: ¿Es ético negarle un programa a alguien que lo necesita para tener un grupo de control? La solución habitual: aleatorización por fases (phase-in design), donde todos eventualmente reciben el programa.
- Viabilidad: No puedes aleatorizar muchas intervenciones (políticas macroeconómicas, reformas constitucionales, guerras).
- Validez externa: Que algo funcione en un contexto no significa que funcione en otro. Un RCT en Kenia no te dice qué pasará en Bolivia (Deaton & Cartwright, 2018).
- Efectos de derrame (spillovers): Si el tratamiento afecta también al grupo de control (porque viven al lado), tu estimación se contamina.
- Cumplimiento imperfecto: No todos los asignados al tratamiento lo reciben, ni todos los del control se quedan fuera.
- Efecto Hawthorne: Los participantes cambian su comportamiento simplemente porque saben que están siendo observados.
- Atrición: Personas que abandonan el estudio. Si la atrición es diferencial (más gente se va del grupo de control que del tratamiento), pierdes la comparabilidad.
14.3.6 Amenazas a la validez de un RCT
Incluso un RCT bien diseñado puede fallar. Estas son las amenazas más comunes:
| Amenaza | Qué es | Cómo detectarla |
|---|---|---|
| Atrición diferencial | Más abandono en un grupo que en otro | Comparar tasas de atrición; test de balance con la muestra final |
| Contaminación | El grupo de control accede al tratamiento | Monitorear adherencia; diseño geográficamente separado |
| Spillovers | El tratamiento afecta al control | Aleatorizar a nivel de cluster; medir exposición |
| Efecto Hawthorne | Cambio de comportamiento por observación | Grupo de control activo (placebo) |
| Incumplimiento | Asignados al tratamiento no participan | Reportar ITT y TOT; analizar compliers |
| Desbalance accidental | Mala suerte en la aleatorización | Balance check pre-intervención; estratificación |
14.4 Diferencia en diferencias (Diff-in-Diff)
14.4.1 La idea
Si no puedes aleatorizar, pero tienes datos de antes y después para un grupo tratado y uno no tratado, puedes estimar el impacto comparando el cambio en ambos grupos.
La lógica: el grupo de control te muestra cómo habría evolucionado el grupo tratado si no hubiera recibido la intervención.
14.4.2 El supuesto clave: tendencias paralelas
Para que diff-in-diff funcione, necesitas asumir que ambos grupos habrían seguido tendencias paralelas sin la intervención. No necesitan tener el mismo nivel, pero sí la misma trayectoria.
¿Cómo verificar este supuesto? No puedes probarlo directamente (porque el contrafactual es, por definición, no observable). Pero puedes verificar si las tendencias eran paralelas antes de la intervención. Si lo eran, es razonable asumir que habrían seguido así.
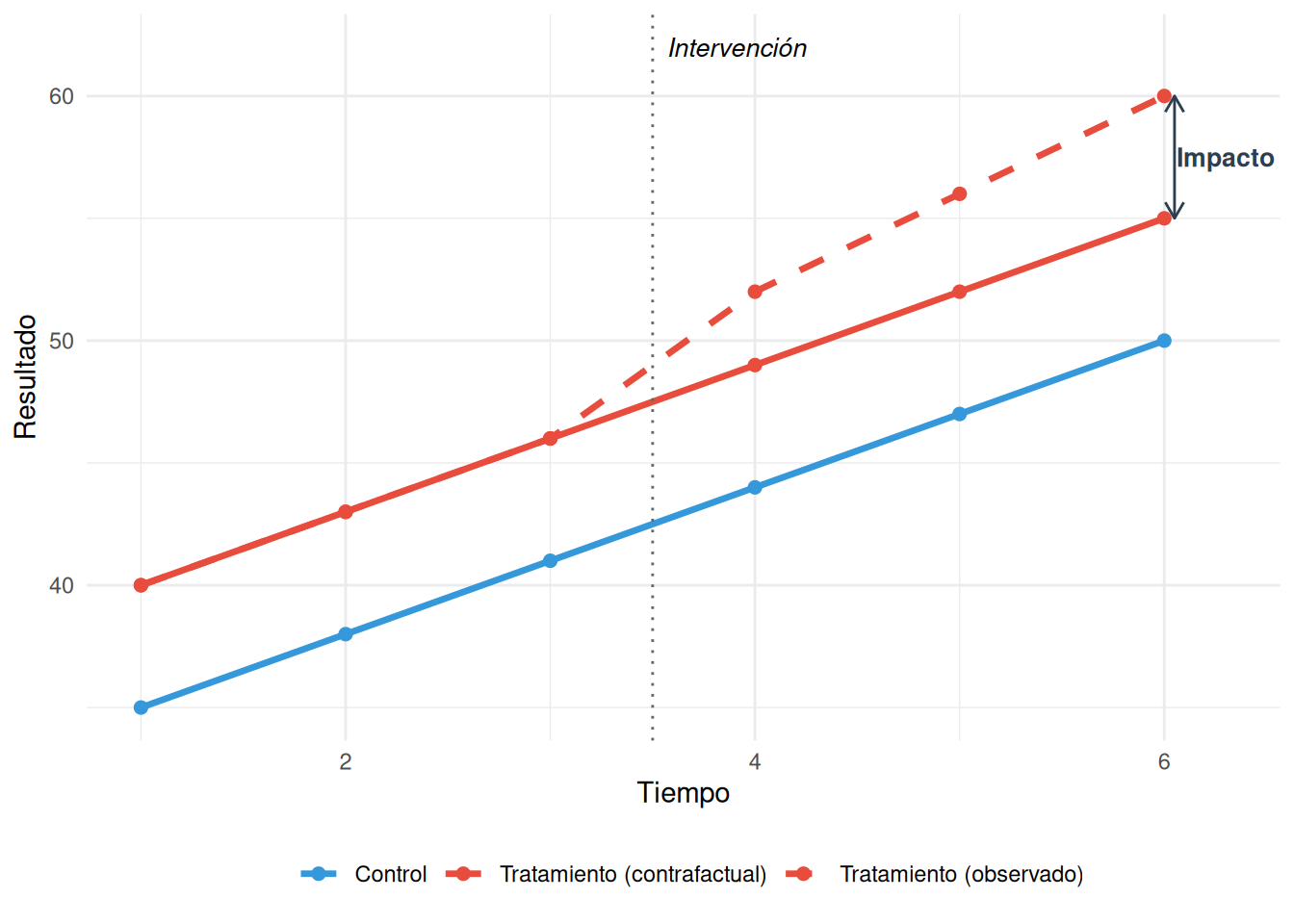
14.4.3 Ejemplo latinoamericano
¿El programa Jornada Escolar Completa (JEC) en Chile mejoró los resultados SIMCE? Compara las escuelas que adoptaron la jornada completa (tratadas) con las que no (control), antes y después de la implementación. Si las tendencias de puntaje eran paralelas antes de JEC, la diferencia en la evolución post-JEC estima el impacto.
14.4.4 Variantes modernas
La investigación reciente ha mostrado que el DiD clásico puede tener problemas serios cuando el tratamiento se implementa en momentos diferentes (staggered adoption). Métodos nuevos (Callaway & Sant’Anna, Sun & Abraham, de Chaisemartin & D’Haultfœuille) corrigen estos problemas. Si tu tratamiento se implementa en fases, investiga estas alternativas.
14.4.5 Peligros
- Si las tendencias no eran paralelas antes de la intervención, tu estimación está sesgada. Siempre grafica las tendencias pre-intervención.
- Eventos contemporáneos (shocks) que afectan solo a un grupo invalidan el diseño.
- Composición cambiante: si la población del grupo tratado cambia después de la intervención (migración, por ejemplo), estás comparando grupos diferentes.
14.5 Regresión discontinua (RDD)
14.5.1 La idea genial
Muchas políticas usan un puntaje de corte para decidir quién recibe el beneficio. Si sacas más de 60 puntos en la prueba de pobreza, no recibes el programa. Si sacas menos de 60, sí.
La clave: las personas que sacaron 59 y las que sacaron 61 son prácticamente iguales. La única diferencia es que unas recibieron el programa y las otras no. Comparándolas, puedes estimar el efecto del programa.
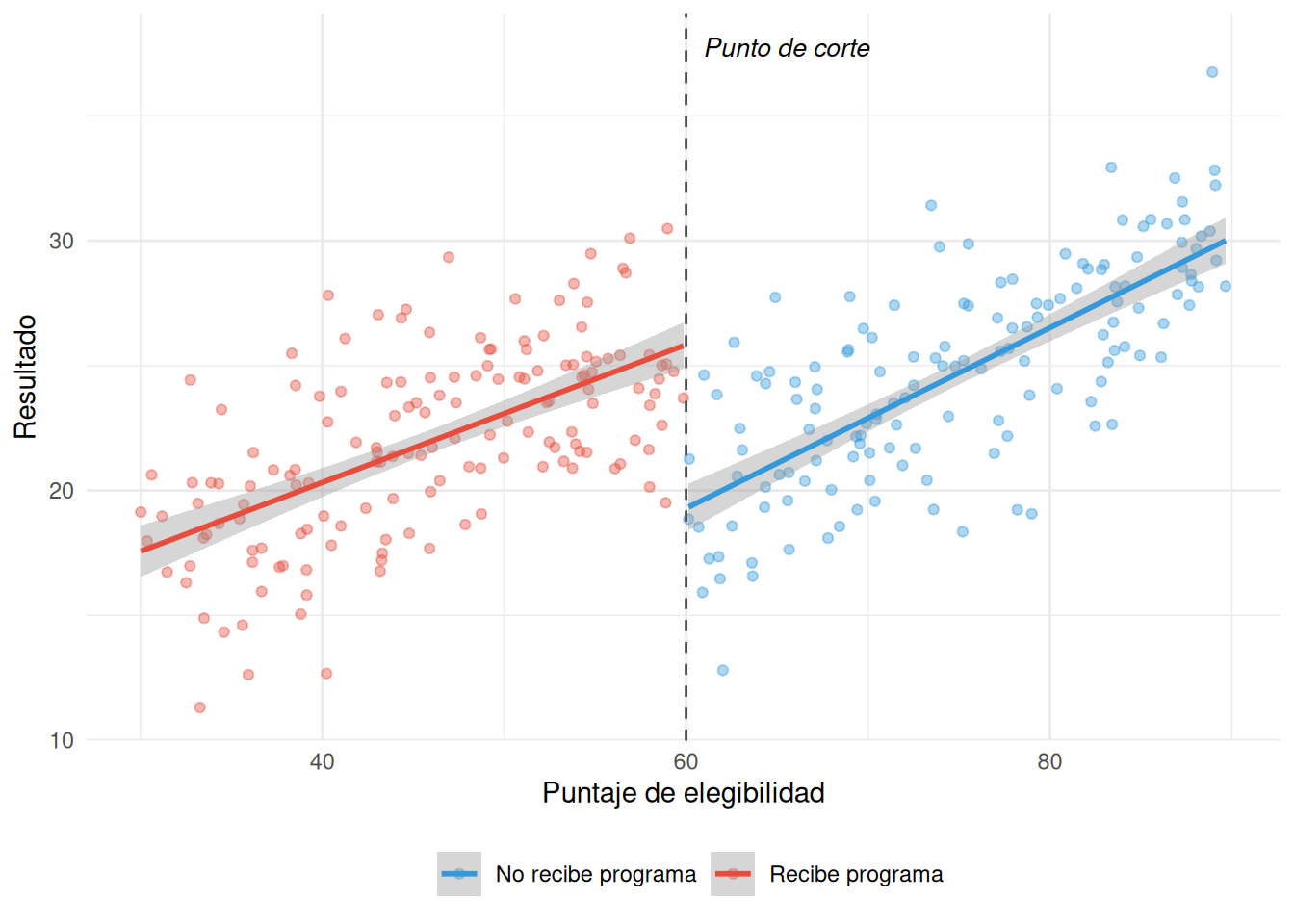
14.5.3 Ejemplos en América Latina
- SISFOH en Perú: El Sistema de Focalización de Hogares asigna un puntaje de pobreza. Los que están debajo del umbral acceden a programas como Juntos o Pensión 65. RDD ideal.
- Becas Pell en EE.UU. (pero aplicable a PRONABEC en Perú): Becas basadas en puntaje. Efecto sobre graduación.
- Cuotas de género en concejos municipales: En algunos países, la proporción de mujeres electas cambia discontinuamente según el tamaño del concejo.
14.5.4 ¿Cuándo funciona?
- Cuando el corte es arbitrario (no manipulable por los participantes).
- Cuando no hay saltos en otras variables en el punto de corte.
- Cuando hay suficientes observaciones cerca del corte.
14.5.5 ¿Cuándo no funciona?
Si la gente puede manipular su puntaje para caer justo debajo del corte, el diseño se invalida. Hay un test para esto: el test de McCrary, que verifica si hay una densidad inusual de observaciones justo debajo del corte.
AdvertenciaCuidado con el ancho de banda
En RDD, el resultado es local: solo aplica para personas cerca del corte. No puedes decir que el efecto es el mismo para alguien con 30 puntos que para alguien con 59. Y la elección del ancho de banda (¿cuán “cerca” del corte?) afecta tus resultados. Usa métodos de selección óptima de ancho de banda (Calonico, Cattaneo & Titiunik) y reporta la sensibilidad a diferentes anchos.
14.6 Matching y Propensity Score
14.6.1 El problema
En estudios observacionales, el grupo tratado y el no tratado suelen ser diferentes en características que también afectan el resultado. Los que participan en un programa de capacitación son más motivados, más jóvenes, más educados, etc.
14.6.2 La solución
Emparejar a cada persona tratada con una persona no tratada que sea lo más similar posible en todas las características relevantes.
El Propensity Score Matching (PSM) resume todas las características en un solo número: la probabilidad de ser tratado dada las características observables. Luego emparejas personas con probabilidades similares.
14.6.3 Tipos de matching
| Tipo | Cómo funciona | Ventaja | Desventaja |
|---|---|---|---|
| Exacto | Empareja con valores idénticos en todas las covariables | Máxima precisión | Imposible con muchas variables continuas |
| Nearest neighbor | El control más parecido en propensity score | Simple, intuitivo | Puede emparejar observaciones lejanas |
| Caliper | Nearest neighbor pero con distancia máxima | Evita malos emparejamientos | Puede perder muchas observaciones |
| Kernel | Promedio ponderado de todos los controles | Usa toda la información | Sensible a la elección del kernel |
| CEM (Coarsened Exact Matching) | Discretiza variables y empareja exacto | Reduce dependencia del modelo | Puede perder muchas observaciones |
14.6.4 Pasos para un buen PSM
- Estima el propensity score con un modelo logit o probit (la variable dependiente es ser tratado o no).
- Verifica el soporte común (common support): ¿hay observaciones de control con probabilidades similares a las de los tratados? Si no las hay, tu matching no funciona.
- Empareja usando alguno de los métodos de la tabla.
- Verifica el balance post-matching: las covariables deben ser estadísticamente iguales entre tratados y controles emparejados.
- Estima el efecto comparando resultados entre los emparejados.
14.6.5 Limitación brutal
PSM solo controla por variables observables. Si hay una variable importante que no mediste (motivación, conexiones, suerte), tu estimación está sesgada. Y nunca sabes con certeza si hay variables omitidas. Como dice el refrán econométrico: “Selection on observables is a strong assumption.”
14.7 Variables instrumentales: la salida creativa
14.7.1 El concepto
A veces tienes una variable (el “instrumento”) que afecta tu variable independiente pero no afecta directamente tu variable dependiente (solo a través de la independiente). Formalmente, un instrumento \(Z\) debe cumplir:
- Relevancia: \(Z\) está correlacionado con la variable endógena \(X\). (Verificable estadísticamente.)
- Exclusión: \(Z\) afecta \(Y\) solo a través de \(X\). (No verificable directamente. Requiere argumento teórico.)
- Independencia: \(Z\) no está correlacionado con los factores no observados que afectan \(Y\).
14.7.2 El ejemplo clásico
¿La educación aumenta los ingresos? El problema es que las personas más hábiles tienen más educación Y más ingresos. ¿Es la educación o la habilidad?
Angrist & Pischke (2009) usaron el trimestre de nacimiento como instrumento: por las leyes de edad mínima para dejar la escuela, los nacidos en ciertos trimestres tienen ligeramente más educación. El trimestre de nacimiento no afecta los ingresos directamente, solo a través de la educación.
14.7.3 Otros instrumentos famosos
| Instrumento | Variable endógena | Resultado | Autor |
|---|---|---|---|
| Distancia a la universidad | Años de educación | Ingresos | Card (1995) |
| Lluvia | Conflicto civil (vía ingreso agrícola) | Violencia | Miguel et al. (2004) |
| Tipo de río (navegable) | Instituciones coloniales | Desarrollo actual | Acemoglu et al. (2001) |
| Lotería de servicio militar | Servicio militar | Ingresos | Angrist (1990) |
14.7.4 Instrumentos débiles: el peligro silencioso
Un instrumento que está débilmente correlacionado con \(X\) (baja relevancia) genera estimaciones sesgadas, inconsistentes, y con intervalos de confianza absurdamente amplios. La regla de Staiger-Stock dice que el F-estadístico de la primera etapa debe ser mayor a 10 como mínimo. Si no lo cumple, tu instrumento es débil y tus resultados no son confiables.
14.7.5 El problema
Buenos instrumentos son extremadamente difíciles de encontrar. La mayoría de los que se proponen son cuestionables. Si tu instrumento es malo, tus resultados son peores que un simple OLS. Como dicen Angrist y Pischke: “Better no instrument than a bad instrument.”
14.8 Control sintético: el contrafactual a medida
14.8.1 Una idea elegante
¿Qué pasa cuando el “tratamiento” es un evento único que afecta a una sola unidad? Por ejemplo: ¿cuál fue el efecto de la nacionalización de los hidrocarburos en Bolivia (2006) sobre el crecimiento económico?
No puedes hacer un RCT. No tienes un grupo de control natural para diff-in-diff. Pero puedes construir una Bolivia sintética: una combinación ponderada de otros países latinoamericanos que replica la trayectoria de Bolivia antes de la nacionalización. La diferencia entre la Bolivia real y la Bolivia sintética después de 2006 estima el efecto (Abadie et al., 2010).
14.8.2 Cómo funciona
- Elige un conjunto de países “donantes” (que no hayan tenido un evento similar).
- El algoritmo encuentra los pesos óptimos que hacen que la combinación ponderada replique la trayectoria pre-intervención del país tratado.
- La diferencia post-intervención entre el país real y el sintético es el efecto estimado.
14.8.3 Ventajas
- Transparente: puedes ver exactamente qué países y con qué pesos se usa para el contrafactual.
- Aplica cuando N = 1 (un solo caso tratado).
- No requiere tendencias paralelas estrictas (como DiD).
14.8.4 Limitaciones
- Necesitas buenos datos pre-intervención para construir un buen sintético.
- Si ninguna combinación de donantes replica la trayectoria pre-intervención, el método no funciona.
- La inferencia estadística es complicada (se usan tests de permutación).
14.9 ¿Cuál método elegir?
| Método | Necesitas | Supuesto clave | Fortaleza | Debilidad |
|---|---|---|---|---|
| RCT | Poder aleatorizar | Aleatorización exitosa | Máxima credibilidad causal | Costoso, no siempre viable, validez externa limitada |
| Diff-in-Diff | Datos pre/post, grupo control | Tendencias paralelas | Usa datos observacionales | Supuesto no testeable directamente |
| RDD | Puntaje de corte | No manipulación del corte | Causalidad local creíble | Efecto solo local (cerca del corte) |
| PSM | Muchas covariables | Sin variables omitidas | Flexible, intuitivo | No controla inobservables |
| Var. instrumentales | Un buen instrumento | Exclusión e independencia | Creativo, potente | Instrumentos buenos son raros |
| Control sintético | Datos panel pre/post | Buen ajuste pre-intervención | Transparente, N = 1 | Inferencia difícil |
14.9.1 La “escalera de credibilidad”
En la práctica, los investigadores hablan de una jerarquía de credibilidad causal:
- RCT → Máxima credibilidad (si está bien ejecutado)
- RDD → Alta credibilidad (cuasi-experimental natural)
- DiD → Credibilidad moderada-alta (depende de las tendencias)
- IV → Credibilidad variable (depende del instrumento)
- PSM → Credibilidad moderada (solo controla observables)
- Antes/después sin control → Baja credibilidad
- Comparación transversal sin diseño → Mínima credibilidad
AdvertenciaCuidado con la “evaluacionitis”
No todo necesita un RCT. No todo puede ser evaluado con métodos experimentales. A veces, un buen estudio descriptivo o un análisis cualitativo profundo aporta más que una evaluación de impacto mal diseñada. La obsesión por la “evidencia rigurosa” (léase: RCTs) ha llevado a algunos a creer que solo los RCTs producen conocimiento válido. Deaton & Cartwright (2018) son particularmente elocuentes sobre los peligros de esta postura.
ImportanteReflexión
Ningún método es perfecto. Todos tienen supuestos. La clave no es encontrar el método “correcto”, sino ser honesto sobre los supuestos que estás haciendo y qué tan razonables son en tu contexto. Un investigador que dice “este método tiene estas limitaciones” es infinitamente más creíble que uno que presenta sus resultados como verdad revelada.
TipEjercicio
- Piensa en una política pública que conozcas (puede ser un programa de tu país). ¿Cómo la evaluarías? ¿Qué método usarías y por qué?
- Para esa misma política, identifica: ¿cuál es el contrafactual? ¿Cuál es el supuesto clave de tu método? ¿Es razonable en este contexto?
- Busca una evaluación de impacto publicada (J-PAL, 3ie, o el Banco Mundial tienen repositorios) y evalúa críticamente: ¿cumplen con sus supuestos? ¿Reportan amenazas a la validez?
- Si tuvieras que explicar la diferencia entre ITT y TOT a alguien que no sabe de evaluación, ¿qué ejemplo usarías?
Abadie, A., Diamond, A., & Hainmueller, J. (2010). Synthetic Control Methods for Comparative Case Studies: Estimating the Effect of California’s Tobacco Control Program. Journal of the American Statistical Association, 105(490), 493-505.
Angrist, J. D., & Pischke, J.-S. (2009). Mostly Harmless Econometrics: An Empiricist’s Companion. Princeton University Press.
Deaton, A., & Cartwright, N. (2018). Understanding and Misunderstanding Randomized Controlled Trials. Social Science & Medicine, 210, 2-21.
Gertler, P. J., Martinez, S., Premand, P., Rawlings, L. B., & Vermeersch, C. M. J. (2016). Impact Evaluation in Practice (2nd ed.). World Bank Group.